Kutta–Joukowski theorem
The Kutta–Joukowski theorem is a fundamental theorem of aerodynamics. It is named after the German Martin Wilhelm Kutta and the Russian Nikolai Zhukovsky (or Joukowski) who first developed its key ideas in the early 20th century. The theorem relates the lift generated by a right cylinder to the speed of the cylinder through the fluid, the density of the fluid, and the circulation. The circulation is defined as the line integral, around a closed loop enclosing the cylinder or airfoil, of the component of the velocity of the fluid tangent to the loop.[1] The magnitude and direction of the fluid velocity change along the path.
The flow of air in response to the presence of the airfoil can be treated as the superposition of a translational flow and a rotational flow. It is, however, incorrect to think that there is a vortex like a tornado encircling the cylinder or the wing of an airplane in flight. It is the integral's path that encircles the cylinder, not a vortex of air. (In descriptions of the Kutta–Joukowski theorem the airfoil is usually considered to be a circular cylinder or some other Joukowski airfoil.)
The theorem refers to two-dimensional flow around a cylinder (or a cylinder of infinite span) and determines the lift generated by one unit of span. When the circulation 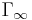 is known, the lift
is known, the lift 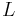 per unit span (or
per unit span (or 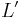 ) of the cylinder can be calculated using the following equation:[2]
) of the cylinder can be calculated using the following equation:[2]
- (1)
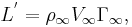
where 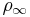 and
and 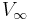 are the fluid density and the fluid velocity far upstream of the cylinder, and
are the fluid density and the fluid velocity far upstream of the cylinder, and 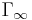 is the circulation defined as the line integral,
is the circulation defined as the line integral,
around a path 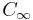 (in the complex plane) far from and enclosing the cylinder or airfoil. This path must be in a region of potential flow and not in the boundary layer of the cylinder. The
(in the complex plane) far from and enclosing the cylinder or airfoil. This path must be in a region of potential flow and not in the boundary layer of the cylinder. The 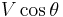 is the component of the local fluid velocity in the direction of and tangent to the curve
is the component of the local fluid velocity in the direction of and tangent to the curve 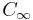 and
and 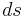 is an infinitesimal length on the curve,
is an infinitesimal length on the curve, 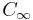 . Equation (1) is a form of the Kutta–Joukowski theorem.
. Equation (1) is a form of the Kutta–Joukowski theorem.
Kuethe and Schetzer state the Kutta–Joukowski theorem as follows:[3]
- The force per unit length acting on a right cylinder of any cross section whatsoever is equal to
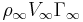 , and is perpendicular to the direction of
, and is perpendicular to the direction of 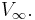
Contents |
Derivation
Two derivations are presented below. The first is a heuristic argument, based on physical insight. The second is a formal and technical one, requiring basic vector analysis and complex analysis.
Heuristic argument
For a rather heuristic argument, consider a thin airfoil of chord  and infinite span, moving through air of density
and infinite span, moving through air of density  . Let the airfoil be inclined to the oncoming flow to produce an air speed
. Let the airfoil be inclined to the oncoming flow to produce an air speed  on one side of the airfoil, and an air speed
on one side of the airfoil, and an air speed 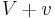 on the other side. The circulation is then
on the other side. The circulation is then
The difference in pressure 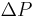 between the two sides of the airfoil can be found by applying Bernoulli's equation:
between the two sides of the airfoil can be found by applying Bernoulli's equation:
so the lift force per unit span is
A differential version of this theorem applies on each element of the plate and is the basis of thin-airfoil theory.
Formal derivation
-
Formal derivation of Kutta–Joukowski theorem First of all, the force exerted on unit unit length of a cylinder of arbitrary cross section is calculated.[4] Let this force per unit length (from now on referred to simply as force) be 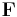 . So then the total force is:
. So then the total force is:
where C denotes the borderline of the cylinder,
 is the static pressure of the fluid,
is the static pressure of the fluid, 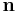 is the unit vector normal to the cylinder, and ds is the arc element of the borderline of the cross section. Now let
is the unit vector normal to the cylinder, and ds is the arc element of the borderline of the cross section. Now let 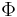 be the angle between the normal vector and the vertical. Then the components of the above force are:
be the angle between the normal vector and the vertical. Then the components of the above force are:Now comes a crucial step: consider the used two-dimensional space as a complex plane. So every vector can be represented as a complex number, with its first component equal to the real part and its second component equal to the imaginary part of the complex number. Then the force F can be represented as:
The next step is to take the complex conjugate of the force F and do some manipulation:
Surface segments ds are related to changes dz along them by:
Plugging this back into the integral, the result is:
Now the Bernoulli equation is used, in order to remove the pressure from the integral. Throughout the analysis it is assumed that there is no outer force field present. The mass density of the flow is
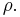 Then pressure p is related to velocity v by:
Then pressure p is related to velocity v by:With this the force F becomes:
Only one step is left to do: introduce
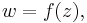 the complex potential of the flow. This is related to the velocity components as
the complex potential of the flow. This is related to the velocity components as 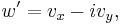 where the apostrophe denotes differentiation with respect to the complex variable z. After some manipulation, the desired expression for the force is obtained:
where the apostrophe denotes differentiation with respect to the complex variable z. After some manipulation, the desired expression for the force is obtained:which is called the Blasius–Chaplygin formula.
To arrive at the Joukowski formula, this integral has to be evaluated. From complex analysis it is known that a holomorphic function can be presented as a Laurent series. From the physics of the problem it is deduced that the derivative of the complex potential w will look thus:
The function does not contain higher order terms, since the velocity stays finite at infinity. So
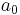 represents the derivative the complex potential at infinity:
represents the derivative the complex potential at infinity: 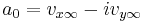 . The next task is to find out the meaning of
. The next task is to find out the meaning of 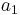 . Using the residue theorem on the above series:
. Using the residue theorem on the above series:Now perform the above integration:
The first integral is recognized as the circulation denoted by
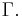 The second integral can be evalutated after some manipulation:
The second integral can be evalutated after some manipulation:Here
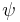 is the stream function. Since the C border of the cylinder is a streamline itself, the stream function does not change on it
is the stream function. Since the C border of the cylinder is a streamline itself, the stream function does not change on it 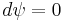 . Hence the above integral is zero. As a result:
. Hence the above integral is zero. As a result:Take the square of the series:
Plugging this back into the Blasius–Chaplygin formula, and performing the integration using the residue theorem:
And so the Kutta–Joukowski formula is:
See also
Notes
References
- Batchelor, G. K. (1967) An Introduction to Fluid Dynamics, Cambridge University Press
- Clancy, L.J. (1975), Aerodynamics, Pitman Publishing Limited, London ISBN 0 273 01120 0
- A.M. Kuethe and J.D. Schetzer (1959), Foundations of Aerodynamics, John Wiley & Sons, Inc., New York ISBN 0 471 50952 3
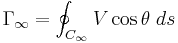
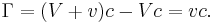
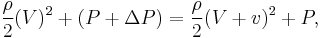
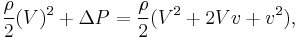
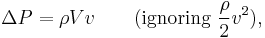
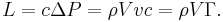
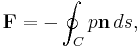
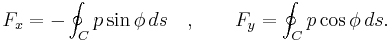
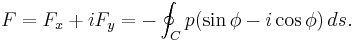
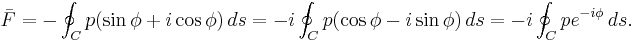
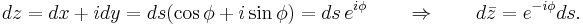
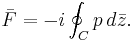
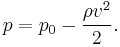
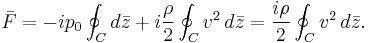
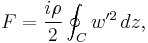
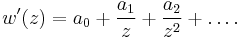
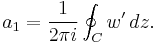
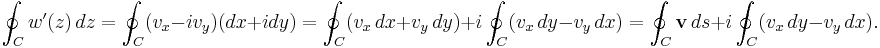
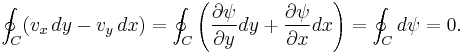
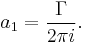
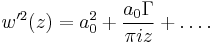
![{F}=\frac{i\rho}{2}\left[2\pi i \frac{a_0\Gamma}{\pi i}\right]=i\rho a_0 \Gamma = i\rho \Gamma(v_{x\infty}-iv_{y\infty})=\rho\Gamma v_{y\infty}%2B i\rho\Gamma v_{x\infty}=F_x%2BiF_y.](/2012-wikipedia_en_all_nopic_01_2012/I/afbc6ac2e73fdeb3e78b20ca78c695bc.png)
